Геометрія 8 клас

 Дистанційне навчання

Свої фотозвіти можна надсилати на пошту       sogfi1963@gmail.com

https://meet.google.com/hpp-zayg-m

УРОК -ОНЛАЙН

9 травня

Тема: Подібність трикутників (повторення).

Домашня робота:

4 травня

Тема:Многокутники та їх властивості.

Повторення.

1. Сума кутів чотирикутника дорівнює ...

2. Знайдіть кути чотирикутника ,якщо їх градусні міри відносяться як 10:4:3:1. Опуклий чи неопуклий є цей чотирикутник ?

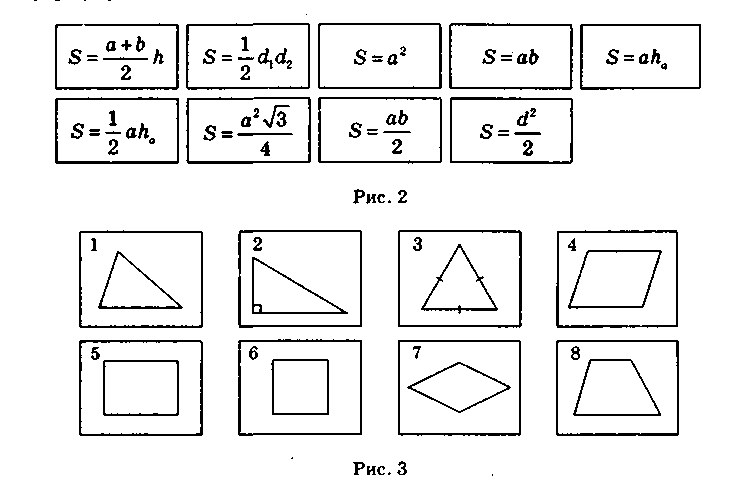
3. Для яких чотирикутників, виконуються ці умови ?

4. Цей чотирикутник є опуклим, протилежні сторони рівні ,сума будь -яких двох сусідніх кутів дорівнює 1800; діагоналі точкою перетину діляться навпіл.

5. Що можна сказати про вид паралелограма , коли відомо що він має три рівних кути .

6. Периметр прямокутникуа дорівнює 40 см. Знайдіть його сторони ,коли відомо , що одна з них на 5 см більше за другу .

7.Знайдіть кути ромба ,якщо сума двох його кутів дорівнює 2100

8. Чотирикутник у якого дві сторони паралельні ,а дві інші не паралельні називають...

9.. Знайдіть площу ромба з діагоналями 34 см і 40 см.

Домашнє завдання:

2 травня

Тема:Площі многокутників

Перекресліть фігури та поруч запишіть формулу

 для обчислення її площі.

 Розв"язування задач.

1.     Визначте кількість сторін опуклого многокутника,

 сума кутів яко­го дорівнює 1 080°.

2.     Площа квадрата дорівнює 144 см². Знайдіть площу 

прямокутника, ширина якого менша від сторони квадрата

 на 2 см, а довжина біль­ша за сторону квадрата удвічі.

3.     У рівнобедреному трикутнику бічна сторона відноситься 

до осно­ви як     5 : 6. Знайдіть площу трикутника, 

якщо висота, проведена до основи, дорівнює 8 см.

4.     Знайдіть кути ромба, якщо його висота дорівнює 5 см,

 а площа — 50см².

20 квітня

Тема:  Розв"язування задач.

Самостійна робота.

Самостійна робота

на тему “Площі многокутників (квадрат, прямокутник, паралелограм, трикутник)”

Питання №1

Знайдіть сторону квадрата, якщо його площа дорівнює 100 см2

Питання №2

Знайдіть площу паралелограма, якщо висота дорівнює 15 см,

а сторона до якої проведено висоту – 10 см

Питання №3

Знайдіть площу трикутника, якщо висота дорівнює 9 см, 

а сторона до якої проведено висоту –14 см.

Питання №4

Площа паралелограма дорівнює 80 см2, а висота паралелограма дорівнює 5 см. Знайдіть сторону до якої проведена висота паралелограма.

Питання №5

Периметр квадрата дорівнює 32 см. Знайдіть площу квадрата.

Питання №6

Знайдіть площу прямокутного трикутника, катети

якого дорівнюють 16 см і 12 см.

Питання №7

Сторони прямокутника відносять одна до одної як 2 : 3,

а площа прямокутника дорівнює 24см2. Знайдіть периметр даного прямокутника

Питання №8

Одна із сторін паралелограма дорівнює 5 см, а висота, проведена до другої сторони дорівнює

30 см. Знайдіть периметр паралелограма, якщо його площа дорівнює 90 см2.

Питання №9

Периметр прямокутника 50 см, а одна із сторін на 5 см більша за іншу. Знайдіть площу прямокутника.

Обов"язково малюнок та дані на малюнку,

 поруч записати  що знайти, відповідь.

Для учнів середнього та високого рівня.

1. Формула для обчислення площі:

    а)  трикутника;   б) ромба;  в) паралелограма;   г) трапеції.

2. Знайти площу ромба, сторона якого 8 см, а висота – 7 см..

а) 32 см²;      б) 28 см²;       в) 56 см²;        г) 87 см².

3. Обчислити площу прямокутника зі сторонами 6 см і 8,5 см.

а) 15,5 см²;      б) 25,5 см²;       в) 48,5 см²;        г) 51 см².

4. Знайти площу прямокутного трикутника з гіпотенузою 12 см, у якого один з кутів рівний 60⁰.

а)  інше - ? см²;      б) 72 см²;       в)  см²;        г) 6 см².

5. Більша сторона паралелограма дорівнює 10 см, а його висоти 3 см і 5 см. Знайти меншу сторону паралелограма.

6. Бісектриса кута прямокутника ділить сторону на відрізки пропорційні числам 1 і 3. Обчислити площу прямокутника, якщо його діагональ рівна 15 см.

7. Знайдіть площу рівнобічної трапеції, у якої більша основа дорівнює 6 см, бічна сторона – 3 см, а діагональ – 5 см.

18 квітня

Тема:Площа трапеції. Розв"язування задач.

Перевіримо знання      -    ТЕСТ площа трапеції 

1) Основи рівнобедреної трапеції дорівнюють 8см і 16см, а гострі кути 45^о. Знайдіть площу трапеції.

Дано: ABCD – рівнобічна трапеція (BC||AD)

АВ=CD; ВС=8см; AD=16см; <A=<D=45⁰.

Знайти: S.

2) Знайдіть площу прямокутної трапеції з бічними сторонами 12см і 13см, діагональ якої є бісектрисою гострого кута.

Дано: ABCD – прямокутна трапеція (BC||AD)

АВ=12см; CD=13см; DB - бісектриса

Знайти: S.

Домашня робота. Вивчити властивості та формули для трапеції.

Виконати Ірівень №982, 984

                   ІІрівень №989, 991.

 

Площа трикутника ТЕСТ

6 квітня

Тема: Площа трикутника.

Перегляньте уважно відео 1 та відео 2 до домашнього завдання.

Прочитайте  параграф 25.

Повторіть теорему про площу трикутника та наслідки 1 - 3.

Розгляньте задачі 1 - 3, розв'язані в підручнику.

За зразком у відео розв'яжіть: усно № 940 (у відео № 1);

                                                   письмово № 945; № 955 (у відео № 3).

відео 1

відео 2

Домашнє завдання:  Малюнки, дано, знайти, розв"язання-обов"язково!

№956 (підказка: скласти рівняння Х і 4Х) з описом.

№963 (підказка: 1) знайти гіпотенузу за т.Піфагора. 2) знайти площу за катетами.

3) знайти висоту проведену до гіпотенузи.)

4 квітня

Тема: Площа трикутника.

Задача. На дошці зображено дві фігури: паралелограм ABCD і трикутник MNK такі, що AD = МК, і висоти проведені до цих сторін (ВН, NF), також рівні (див. рис).

Площа паралелограма відома. Як знайти площу трикутника?

Задачі за готовим рисунком: Знайти площу трикутника.

 Знайдіть площу:

а) рівнобедреного трикутника з основою 10 см і бічною стороною 13 см;

б) трикутника ABC, в якому  АВ = 17 см, а висота ВН ділить сторону АС на відрізки АН = 8 см і НС = 2 см.

3.   Площа трикутника дорівнює 72 см2. Знайдіть периметр трикутника, якщо його висоти дорівнюють 9 см, 12 см і 24 см.

4.   Знайдіть площу ромба, діагоналі якого дорівнюють 8 м і 20 м.

5.   Знайдіть площу:

а) трикутника ABC з висотою ВН , якщо АВ= 13 см, ВС = 15 см, ВН = 12 см, а точка Н лежить на відрізку АС;

б) прямокутного трикутника, гіпотенуза якого ділиться висотою на відрізки завдовжки 9 см і 4 см;

в) рівностороннього трикутника з висотою 2 см.

6.   На рисунку 9, 10 подано одиничний квадрат. Знайдіть площу заштрихованої фігури.

Домашнє завдання

Вивчити зміст теореми, її доведення та наслідки.

Розв'язати задачі.

1.   Знайдіть площу:

а) прямокутного трикутника з гіпотенузою 20 см і катетом 12 см;

б) гострокутного трикутника  ABC з висотою AN = 4 см, якщо ВН = 2 см. C = 45°.

2.   Знайдіть гіпотенузу прямокутного трикутника, якщо його площа дорівнює 20 см2. а висота, проведена з вершини прямого кута, — 4 см.

3.   Знайдіть діагоналі ромба, якщо одна з них удвічі більша за другу, а площа ромба дорівнює 64 см2.

4.   Знайдіть площу рівнобедреного трикутника з периметром 16 см і висотою завдовжки 4 см. проведеною до основи.

5.   Накресліть гострокутний трикутник і проведіть у ньому висоту. Проведіть необхідні вимірювання та обчисліть:

а) площу даного трикутника;

б) площі трикутників, на які даний трикутник ділиться висотою.

16 березня

Тема: Площа паралелограма.

Перевіримо знання. Площа квадрата, площа прямокутника.

ТЕСТ 1

Перегляньте уважно ВІДЕО

Прочитайте  параграф 24.

Вивчіть теорему про площу паралелограма.

Розгляньте задачі 1, 2, розв'язані в підручнику.

За зразком у відео розв'яжіть: усно № 914 (у відео № 1);

   письмово № 921 (у відео № 2); № 925 (у відео № 3).

Завдання: №922, 928.                                       

14 березня

Тема:Поняття площі многокутника. Площа прямокутника.

Уважно передивіться ПРЕЗЕНТАЦІЮ

Повторіть  параграф 23.

Повторіть: означення площі многокутника;

                   основні властивості площі;

                  теорему про площу многокутника;

                  наслідок.

Розв'яжіть письмово № 887 (1), № 895.

Самостійна робота.

1 питання (1б.)

Оберіть неправильну властивість площі многокутника.

А) площа кожного многокутника є додатним числом

Б) рівні між собою многокутники мають рівні площі

В)якщо многокутник розбито на кілька многокутників, то його площа дорівнює

добутку площ цих многокутників

Г) якщо многокутник розбито на кілька многокутників, то його площа дорівнює сумі площ цих многокутників

2 питання (1б.)

Оберіть правильний варіант формули для обчислення площі квадрата.

А) S = 4a         Б) S = 2 ∙ (a + b)         В) S = a ∙ b          Г) S = a²

3 питання (1б.)

Оберіть правильний варіант формули для обчислення площі прямокутника.

А) S = 2 ∙ (a + b)        Б) S = a²         В) S = a + b         Г) інша відповідь

4 питання (1б.)

Як називаються многокутники, які мають рівні площі?

А) рівнобедрені      Б) рівнобічні        В) рівносторонні          Г) рівновеликі

5 питання (1б.)

Обчисліть площу прямокутника із сторонами 4 см і 6,5 см. Запишіть обчислення

 А) 21 см²           Б) 20 см²           В) 10,5 см²            Г) 26 см²

6 питання (1б.)

Обчисліть площу квадрата, сторона якого дорівнює 0,5 дм. Запишіть обчислення

А) 2,5 дм²              Б) 0,25 см²             В) 10 дм²             Г) 0,25 дм²

7 питання (2б.)

Знайдіть сторону квадрата, якщо його площа дорівнює 64 см². Запишіть обчислення 

8 питання (2б.)

Периметр прямокутника дорівнює 40 см, а одна із сторін у 3 рази більша за іншу. Знайдіть площу прямокутника у см². Запишіть обчислення

9 питання (2б.)

Знайдіть периметр квадрата ( у см), який рівновеликий прямокутнику із сторонами      4см і 25 см. Запишіть обчислення

******************************************************************************************

1. Як зміниться площа прямокутника, якщо кожну з його сторін зменшити у 10 разів?

2. Квадрат зі стороною 12 см і прямокутник, одна сторона якого дорівнює 8 см, рівновеликі. Знайдіть периметр даного прямокутника.

3. Знайдіть периметр квадрата, якщо його площа дорівнює 64 см2

4. Площа прямокутника дорівнює 27 см2 . Знайдіть сторони прямокутника, якщо одна з них втричі більша за іншу.

 5. Прямокутник зі сторонами 10 дм і 9,5 дм розрізали на квадрати, сторона кожного з яких дорівнює 0,5 дм. Скільки таких квадратів отримали?

6. Знайдіть відношення площ двох квадратів, сторони яких відносяться як 3 : 7.

7. Квітник має форму прямокутника, площа якого дорівнює 5 м2 . Квіти у цьому квітнику висаджені рівномірно, кожна квітка займає площу 250 см2 . Визначте кількість квітів у квітнику.

 8. Керамічну плитку розміром 40 х 40 см продають у коробках. У кожній коробці міститься 1,6 м2 плитки. Скільки плиток у одній коробці? 

9. Стіна кімнати має розміри 6 м х 4 м. Скільки рулонів шпалер потрібно купити, щоб поклеїти дві такі стіни, якщо один рулон шпалер має довжину 15м та ширину 100 см?

2 березня

Тема: Контрольна робота.

 Робота

28 лютого

Тема: Розв"язування прямокутного трикутника.

Перевіримо знання. Значення кутів. ТЕСТ

Задачі на обчислення розв"язуєте у робочих зошитах

23 лютого

Тема: Розв"язування прямокутного трикутника.

Перевіримо знання.

Теорема Піфагора ТЕСТ1

Перегляньте уважно   ВІДЕО

Прочитайте  параграф 21.

Розгляньте чотири види задач на розв'язування

 прямокутних трикутників.

Розв'яжіть письмово 

№ 792 (3) (3  вид задач з відео), 

№ 794 (3) (4 вид задач з відео).

Домашнє завдання:№793(1), 795(1), 797.

16 лютого

Тема:Значення кутів. Розв"язування задач. 

Повтріть означення синуса, косинуса, тангенса прямокутного трикутника;

Перегляньте приклади з відео та виконайте №744, 748,752

Домашнє завдання:№745, 749, 753.

14 лютого

Тема:Значення кутів. Розв"язування задач. 

Перегляньте уважно відео.

Прочитайте  параграф 20.

Вивчіть: означення синуса, косинуса, тангенса прямокутного трикутника;

               співвідношення між сторонами та кутами прямокутного трикутника.

Розгляньте Задачі 1 , 3, розв'язані у підручнику.

Розв'яжіть № 736, 742, 746

Домашнє завдання: 737, 741, 743.

2 лютого

Тема:Перпендикуляр і похила. Розв"язування задач. 

Повторіть§14

У робочому зошиті виконайте  самостійну роботу.

                                           робота   

№3 і 4 можна замінити задачами на "ВИБІР".

"ВИБІР"

1. (1 варіант)    Із точки, взятої на відстані 12 см від прямої, проведено до неї дві похилі. Знайдіть відстань між основами похилих, якщо їх сума дорівнює 28 см, а проекції похилих відносяться як 5 : 9.

2.   (2 варіант)   Із однієї точки до даної прямої проведено дві рівні похилі. Відстань між їх основами 14 см. Визначте проекції похилих на дану пряму.

3.  (1 варіант)    Точка знаходиться на відстані 6 см від прямої. З неї до прямої про­ведено похилу, яка утворює з прямою кут 45°. Знайдіть проекцію похилої на цю пряму.

4.   (2 варіант)   Із точки поза прямою проведено до неї дві похилі; довжина однієї з них дорівнює 25 см, а довжина її проекції — 15 см. Знайдіть дов­жину другої похилої, якщо вона утворює з прямою кут 30°.

5.   (1 варіант)   Із точки до прямої проведено перпендикуляр завдовжки 8 см і дві похилі з довжинами 10 см і 17 см. Знайдіть відстань між основами похилих. Скільки розв'язків має задача?

6.   (2 варіант)   Знайдіть висоту, проведену до найбільшої сторони трикутника зі сторонами 15, 41 і 52.

Домашнє завдання(з фото. Кожен має свій номер).

31 січня

Тема: Перпендикуляр і похила. Властивості.

Перегляньте відео 

Вивчіть властивості ст.142-143.

Виконайте №712, 714

Домашнє завдання №717.

19 січня

ТЕМА: Властивість бісектриси трикутника.

17 січня

ТЕМА: властивості середніх пропорційних

відрізків в прямокутному трикутнику.

Теорема: 1) Висота прямокутного трикутника є середнім пропорційним проекцій катетів на гіпотенузу. CD² = AD ∙ DB.

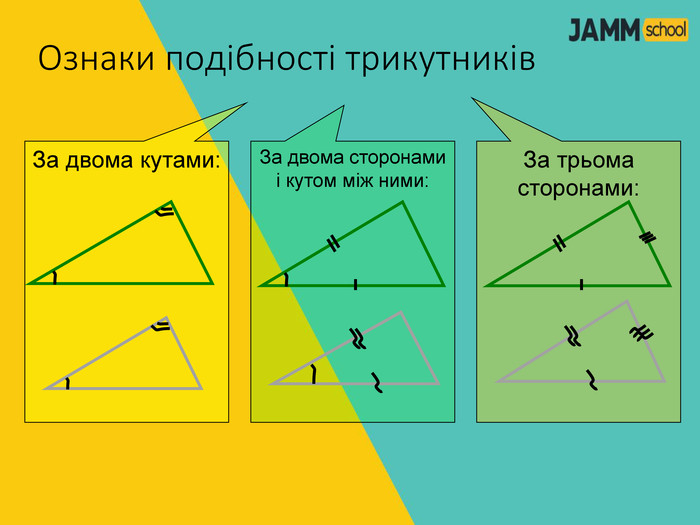
2) Катет прямокутного трикутника є середнім пропорційним гіпотенузи і проекції цього катета на гіпотенузу.

АC² = AD ∙ АB.   CВ² = ВD ∙ АB. 

Розглянемо розв"язки вправ 540 та 542

Розв'яжемо вправи 544 та 546.

Домашнє завдання: Вивчити властивості середніх пропорційних

відрізків в прямокутному трикутнику.

№541, 543, 545, 547.

20 грудня

Тема: Ознаки подібності  трикутників.

 У підручнику прочитайте§14 теореми 1, 2, 3 ст.96, 97, 98

Вивчіть ознаки!

Перша ознака подібності трикутників

1. Якщо два кути одного трикутника відповідно дорівнюють

 двом кутам іншого, то такі трикутники подібні.

Друга ознака подібності трикутників
2. Якщо дві сторони одного трикутника пропорційні двом

 сторонам іншого трикутника і кути, утворені цими

 сторонами рівні, то такі трикутники подібні.

Третя ознака подібності трикутників

3. Якщо три сторони одного трикутника пропорційні 

трьом сторонам іншого, то такі трикутники подібні.

У робочих зошитах виконайте це зображення.

(один трикутник більший , другий-менший)

№486

виконайте малюнок 130 ст. 97- ліворуч.

Праворуч запишіть Дано: (самостійно)

                                 Довести:

Розв"язання

Домашня робота №487.Завдання на повторення на вайбері.

                                                                

                                               

9 грудня

Тема: Подібні трикутники.

Уважно перегляньте   відео

6 грудня

Тема: Узагальнена теорема Фалеса

Уважно перегляньте відео.

З відео запишіть у класній роботі  задачі 1-4.

Прочитайте параграф 12 с. 87-89.

Вивчіть  теорему Фалеса с. 87 та наслідки с.88.

У домашній роботі за зразком у відео розв'яжіть № 474(1, 2)

25 листопада

Тема: Середня лінія трапеції.

Трапеція   Тест 

виконати до 28 листопада до 16год.

Конспект (повторення)

Чотирикутник, у якого дві сторони паралельні, а 

дві інші сторони не паралельні, називається трапецією.

Паралельні сторони трапеції називаються її основами.
AD і BC — основи.

Сторони, які не паралельні, називаються бічними сторонами трапеції.

AB і CD — бічні сторони трапеції.

Прямокутна трапеція       Рівнобічна (рівнобедрена) трапеція

 

Властивості трапеції

1. Сума внутрішніх кутів трапеції (і будь-якого іншого чотирикутника) 

дорівнює  360°.

2. сума кутів, прилеглих до бічної сторони, дорівнює 180°.

Ознаки рівнобедреної трапеції

1. Якщо кути при основі трапеції рівні, то така трапеція рівнобедрена.

 

2. Якщо діагоналі трапеції рівні, то така трапеція рівнобедрена.

Середня лінія трапеції

1. Накресліть довільну трапецію.

2. За допомогою лінійки поділіть бічні сторони пополам.

3. Сполучіть точки поділу.

Відрізок, що сполучає середини бічних сторін трапеції, 

називається середньою лінією трапеції. ЕF-середня лінія

Середня лінія трапеції паралельна основам і дорівнює їх півсумі.

У трапеції лише одна середня лінія.      

EF=BC+AD2

EF∥BC,EF∥AD

Задача 1: Маємо:AE=EB,  CF=FD

     

BC=22 м;

AD= 26 м.

Знайди EF.

Задача 2: Сторони трапеції співвідносяться, як 6:7:6:9,

 а її периметр дорівнює 112 см. Обчисли сторони трапеції.

 Переписати пояснення і задачу 1 та

 2(виконати) у класну роботу, 

Домашня робота::Вивчити конспект (без задач) 

або по підручнику §11,  №328, №331.(невідомий елемент

 позначте за Х

 і складіть та розв'яжіть рівняння).

22 листопада

Тема: Теорема Фалеса

Якщо паралельні прямі, які перетинають сторони кута,

 відтинають на одній його стороні рівні відрізки, 

то вони відтинають рівні відрізки й на іншій його стороні.

.

Якщо прямі паралельні і ВR=RP=PN=NM, то BD=DE=EF.

№283 (дано записуєте самостійно)

Розв'язання

Нехай А1А2=3х см, тоді В1В2=5х см

За теоремою Фалеса А1А2=А2А3, В1В2=В2В3.

Маємо рівняння 3х-2х=8,

                                х=8.

А1А2=А2А3=3*8=24(см)

В1В2=В2В3=5*8=40(см)

Відповідь: 24(см), 24(см),  40(см), 40(см).

Завдання. Переписати пояснення і задачу у класну роботу, 

Домашня робота: вивчити Теорему Фалеса(ст.58)  №284.

18 листопада

Тема: Середня лінія трикутника. 

Означення: Середня лінія трикутника – це відрізок, який сполучає середини двох його сторін. MN – середня лінія трикутника АВС.

 А₁С₁ ІІ АС,  A₁C₁ = 1/2AC .

Властивості: Середня лінія трикутника, яка сполучає середини двох його сторін, паралельна третій стороні. MN ІІ AC . 

Середня лінія трикутника, яка сполучає середини двох його сторін, дорівнює половині третьої сторони.

Завдання для самостійної роботи. 

Задача 1. Визначте вид трикутника, у якому середні лінії рівні між собою. 

Задача 2. Доведіть, що середини сторін чотирикутника є вершинами паралелограма. Задача 3. Сума діагоналей чотирикутника ABCD дорівнює 30 см. Знайдіть периметр чотирикутника, вершини якого є серединами сторін чотирикутника ABCD.

       I.            Домашнє завдання.

 

1.     Опрацювати §10, ст.61-63 вправа №297. 301.

2.     Додаткове завдання: вправа №307..

4листопада

Тема: Розв"язування задач. 

Малюнки та розв"язки до  задач записуєте в зошит.

 Впосані та описані чотирикутники.

Задачі

 Центральні і вписані кути. Описані і вписані чотирикутники

Оберіть правильну відповідь:

1.Знайдіть градусну міру дуги, що становить  кола

А  108°    Б 150°      В 216°    Г 300°

2. Знайдіть вписаний кут, якщо дуга на яку він спирається  44°

А 22°        Б 23°     В  88°     Г 92°

3. Знайдіть дугу, на яку спирається вписаний кут, що дорівнює 42°:

А  21°    Б 24°     В 84°  Г 96°

4. Знайдіть невідомі кути вписаного чотирикутника, якщо 

два його кути дорівнюють 110° і 120°

А  70°  і  50°       Б 70°і 60°     В 70°і 80°     Г 80°і 60°

5. Знайдіть невідому сторону описаного навколо кола чотирикутника, 

якщо три його сторони дорівнюють  7 см, 5 см, 8 см

А  2 см     Б  3 см      В 8 см   Г  10 см

6. Знайти бічну сторону рівнобічної трапеції, якщо середня лінія 

дорівнює 6 см, а периметр 28 см.

А  16 см    Б 14 см   В  7 см    Г   8 см

Домашня робота:

Розв’язати задачі.

7. Трикутник АВС вписаний у коло, центр якого лежить на АВ.

 Знайдіть градусні міри кутів С і В, якщо ∟А=52°.

8. Три кути чотирикутника, вписаного в коло чотирикутника, 

взяті в порядку 

слідування, відносяться як 2:6:7. Знайдіть кути чотирикутника

9.Коло, вписане в рівнобічну трапецію, поділяє точкою дотику 

бічну сторону на відрізки, менший з яких 5 см.

 Знайдіть більшу основу трапеції, якщо її периметр дорівнює 56 см.

 

1 листопада

Тема: Розв"язування задач.  

Малюнки та розв"язки до  задач записуєте в зошит.

1. Центральні та вписані кути. Задачі 

2.  Впосані та описані чотирикутники.

 №263,  265

Домашнє завдання №264, 266.

21 жовтня

Тема: Трапеція.

Перевіримо знання ТЕСТ , №5, 7, 9-письмово(коротко)

Повторіть властивості трапеції на платформі "Мій клас"

№209, 213, 215

Чотирикутники. Дайте відповіді на запитання. 

Відповідь письмово (1-3 слова). Запитання не переписуємо.

1. Чи існує чотирикутник, кути якого дорівнюють 100°, 80°, 135°, 55°?
2. У чотирикутнику ABCD А = С. Чи правильно, що ABCD — пара­лелограм?
3. У паралелограмі ABCD А + С > 180°. Назвіть гострі кути парале­лограма.
4. Діагоналі чотирикутника ABCD перетинаються в точці О, AB = CD, AB || CD. Назвіть пари рівних відрізків з кінцем у точці О.
5. Чи будь-який квадрат є ромбом?
6. Чи правильно, що існує прямокутник, який не є паралелограмом?
7. Три кути паралелограма рівні. Визначте вид паралелограма.
8. Периметр квадрата 24 см. Знайдіть довжини його сторін.
9. Діагоналі паралелограма перпендикулярні. Визначте вид паралелограма.
10. Дві сторони чотирикутника не паралельні. Чи обов’язково цей чотирикутник – трапеція?
11. Як називаються паралельні сторони трапеції?

Завдання:  І рівень №210

                  ІІ  рівень №216

18 жовтня

Тема: Трапеція.

Закінчити речення:

Робота з підручником.

Накресліть трапецію, випишіть її основні елементи 

та властивості ст. 40.

Накресліть у зошиті різні види трапецій (ст.41), підпишіть та запишіть основну властивість, характерну лиш для даної трапеції.

Запишіть теорему ст.42.

Виконайте №196, 202, 207

Самостійно задачі за малюнком:

 

Знайдіть кути трапеції. Знайдіть периметр трапеції.

14 жовтня

Тема:Контрольна робота з теми "Чотирикутники"

                РОБОТА

11 жовтня

Тема: Узагальнення та систематизація знань.

1.  Перевіримо знання-ЧОТИРИКУТНИКИ

        ТЕСТ ( Розв"язки записуємо коротко у зошит)

2.  Виконуємо завдання для перевірки знань ст.39.

4 жовтня

Тема: Квадрат і його властивості.

Перевіримо знання-ПАРАЛЕЛОГРАМ- ТЕСТ

Означення. Прямокутник , у якого всі сторони рівні, називається квадрат.                                   Властивості квадрата.                                                                          1.Протилежні сторони і протилежні кути рівні(властивості паралелограма). 

2. Діагоналі в точці перетину діляться навпіл.( властивості паралелограма).

 3.Діагоналі квадрата рівні(властивість прямокутника).

4. Діагоналі квадрата взаємно перпендикулярні й ділять його кути навпіл

( властивості ромба).

Задача 1(усно) . Сторона квадрата дорівнює 5см. Знайти його периметр, площу.

Задача 2(усно). Діагоналі квадрата MNKP перетинаються в точці S. Назвати усі рівні трикутники, які утворилися при перетині діагоналей. Визначити їх вид.

Задача 3(усно). Знайти кут,який утворює діагональ квадрата з його стороною.

Виконати задачі №161, 163, 164, 177.

Завдання: §5 -вивчити властивості.І рівень-№ 162,164 (рисунок обовязково 

 ІІрівень-№29-35(вайбер, фото)-3задачі на вибір.

 

23 вересня

Тема:Прямокутник і його властивості

Перевіримо знання по темі "Паралелограм"  ТЕСТ 1

Опрацюйте  §3;

Запишіть у зошитах короткий конспект.

Дайте відповідь на запитання  ст.24

1.    Означення прямокутника.

2.   Властивості прямокутника.

3.   Ознаки прямокутника.

Прямокутником називають паралелограм, у якого всі кути прямі.

    Наприклад: паралелограм ABCD – прямокутник, оскільки .

Ознаки прямокутника

1. Якщо у паралелограма один із кутів прямий, то цей паралелограм – прямокутник.
2. Якщо у паралелограма діагоналі рівні, то цей паралелограм – прямокутник.

Властивості прямокутника

     Прямокутник має всі властивості паралелограма, крім того, діагоналі прямокутника рівні.

- відрізок, що з'єднує середину сторони прямокутника з точкою перетину діагоналей, перпендикулярний до цієї сторони і дорівнює половині суміжної сторони прямокутника 

- кут між діагоналями прямокутника вдвічі більший за кут між діагоналями та більшою стороною прямокутника.

Виконайте задачі №84, 89, 96(1)

Завдання: №85,90, (99)

20 вересня

Тема: Паралелограм і його властивості

Перевірка знань. Чотирикутник. ТЕСТ 1

 Паралелограмом називають чотирикутник, у якого протилежні сторони попарно паралельні.

    Наприклад: чотирикутник ABCD – паралелограм, оскільки .

Властивості паралелограма

У паралелограма:

1. Протилежні сторони рівні. AB=CD, AD=BC.
2. Протилежні кути рівні. .
3. Діагоналі точкою перетину діляться навпіл. АО=ОС, ВО=ОD.
4. Кожна діагональ розбиває паралелограм на два рівних трикутники. .
5. Сума кутів, прилеглих до однієї сторони паралелограма, дорівнює 180°. .
6. Сума квадратів діагоналей паралелограма дорівнює сумі квадратів його сторін:  або .

     Висотою паралелограма називають перпендикуляр, опущений із будь-якої точки однієї сторони на пряму, що містить протилежну сторону (або відстань між протилежними сторонами).

    Наприклад: MN і ВК – висоти.

Завдання:

1. Периметр паралелограма дорівнює 24 см. Знайдіть сторони паралелограма, якщо: 

а) одна з них на 2 см більша за іншу;

 б) одна з них утричі менша від іншої;

 в) сума трьох його сторін дорівнює 17 см.

 2. Знайдіть кути паралелограма, якщо:

 а) один з них є прямим;

 б) градусні міри двох кутів відносяться як 2:7;

 в) різниця двох його кутів дорівнює 40°; 

г) сума трьох його кутів дорівнює 330°. 

№57.

6 вересня

Тема: Повторення 

1.У трикутнику MNK MN = NK, MN = 2 см, а периметр трикутника MNK

дорівнює 5 см. Знайдіть сторону MK.

А) 1 см; Б) 2 см; В) 3 см; Г) 4 см.

2. Кут при основі рівнобедреного трикутника становить 130% кута при

вершині. Знайдіть кути трикутника.

А) 50°, 65°, 65°; Б) 55°, 60°, 65°; В) 40°, 60°, 80°; Г) 90°; 30°;60°.

3. Обчисліть довжину кола, якщо його радіус дорівнює 5 см.

А) 20π см; Б) 2,5π см; В) 5π см; Г) 10π см.

4. Кут AOB=164°. Промінь ОС поділяє його на два кути, градусні міри яких

відносяться як 3 : 1. Знайдіть ці кути.

5. У колі з центром О проведено діаметри АВ і СD, АВ = 20 см, АС = 6 см.

Знайдіть периметр ΔBOD.

ПОВТОРИТИ: 

1) Види трикутників;

2) Сума кутів трикутника;

3) Формула довжини кола.

Завдання:

1.У трикутнику EFP   EF = EP, FP = 1,5EF. Периметр трикутникa EFP

дорівнює 7 см. Знайдіть сторону FP.

А) 1 см; Б) 2 см; В) 3 см; Г) 1,5 см.

2. Кут при основі рівнобедреного трикутника в 2 рази більший від кута при

вершині. Знайдіть кути трикутника.

А) 36°, 72°, 72°; Б) 50°, 65°, 65°; В) 80°, 50°, 50°; Г) 90°; 30°;60°.

3. Обчисліть діаметр кола, якщо довжина кола дорівнює 40π см.

А) 20 см; Б) 40 см; В) 80 см; Г) 60 см

4. Промінь MF поділяє розгорнутий кут EMH у відношенні 1 : 2. Знайдіть

ці кути.

5. У колі з центром О проведено діаметр АC і хорду AB, кут ВАС = 40°.

Знайдіть кут ВОС.